FSharp.Charting: BoxPlot Charts

Summary: This example shows how to create boxplot diagrams in F#. It looks at how to create a single boxplot from six statistics about an observation set as well as how to automatically create boxplots from observations.

When creating boxplot charts, it is possible to use either six statistics (Lower whisker, Upper whisker, Lower box, Upper box, Average, Median) that define the boxplot data, or to infer these statistics from a set of values and let the library generate the boxplot diagram automatically.

A boxplot diagram shows six basic statistics about a set of observations. It displays the dataset minimum and maximum, the upper and lower quartiles, the average value, and the median. When the F# script calculates these six statistics, the values can be passed to the method Chart.BoxPlotFromStatistics as a list of tuples to draw multiple boxplots.

1: 
2: 
3: 
4: 
5: 
6:

// On Mac OSX use FSharp.Charting.Gtk.fsx
#I "packages/FSharp.Charting"
#load "FSharp.Charting.fsx"

open FSharp.Charting
open System

1: 
2: 
3:

Chart.BoxPlotFromStatistics( 
    [ ("Result A", -12.7, 11.6, -8.3, 6.4, 0.0, 0.0);
      ("Result B", -6.7, 11.6, -5.0, 5.4, 0.0, 0.0) ])

Chart

Here is the same box plot with dates used as labels. These must be explicitly formatted as strings.

1: 
2: 
3: 
4:

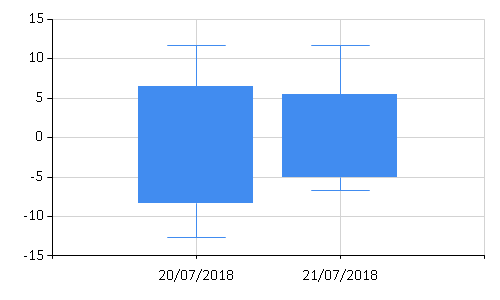
Chart.BoxPlotFromStatistics(
    [ (DateTime.Today.ToShortDateString()             , -12.7, 11.6, -8.3, 6.4, 0.0, 0.0);
      (DateTime.Today.AddDays(1.0).ToShortDateString(), -6.7, 11.6, -5.0, 5.4, 0.0, 0.0) ],
    ShowMedian = false, ShowAverage = false)

Chart

This snippet calls the Chart.BoxPlotFromStatistics method with a list containing
(Label, Lower whisker, Upper whisker, Lower box, Upper box, Average, Median) pairs. The call uses the value 0.0 as a placeholder for the last two statistics. The lines in the boxplot diagram have to be hidden explicitly by setting BoxPlotShowMedian and BoxPlotShowAverage to false.

Another alternative when creating a boxplot is to let the charting library calculate the boxplot statistics automatically. To do that, the Chart.BoxPlot method can be called with a collection of (xLabel, yValues) tuples as an argument. Each entry is a label plus a set of observations. The statistics are automatically computed from the values in the observations.

1: 
2: 
3: 
4: 
5: 
6: 
7:

let date n = DateTime.Today.AddDays(float n).ToShortDateString()
let rnd = new System.Random()

let threeSyntheticDataSets = 
    [ (date 0, [| for i in 0 .. 20 -> float (rnd.Next 20) |])
      (date 1, [| for i in 0 .. 20 -> float (rnd.Next 15 + 2) |])
      (date 2, [| for i in 0 .. 20 -> float (rnd.Next 10 + 5) |]) ]

1: 
2: 
3: 
4:

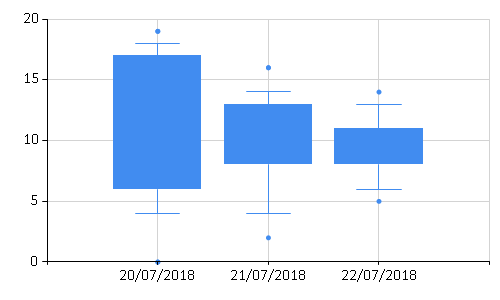
Chart.BoxPlotFromData
  ( threeSyntheticDataSets,
    ShowUnusualValues = true, ShowMedian = false,
    ShowAverage = false, WhiskerPercentile = 10)

Chart

The example above demonstrates how to calculate boxplot diagrams automatically from (randomly generated) data. It is also possible to set several custom properties to configure the boxplot diagram. When BoxPlotShowUnusualValues is true, the boxplot displays unusual values using points, as shown in Figure 1.