Growth curve

Summary: this tutorial demonstrates variou way to model growth curves, a commong task in any (micro)biological lab

Modelling

Growth and other physiological parameters like size/weight/length can be modeled as function of time. Several growth curve models have been proposed. Some of them are covered in this documentation.

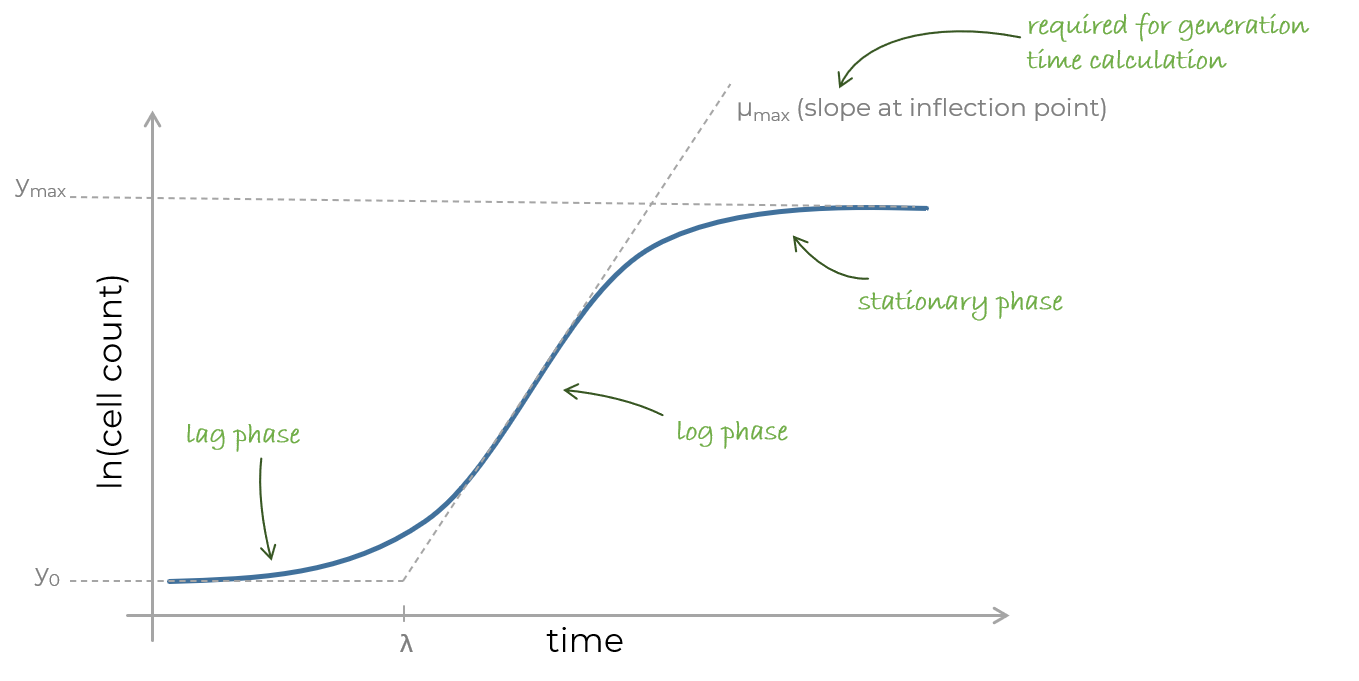
For growth curve analysis the cell count data must be considered in log space. The exponential phase (log phase) then becomes linear. After modeling, all growth parameters (maximal cell count, lag phase duration, and growth rate) can be derived from the model, so there is no need for manual labelling of separate growth phases.

If specific parameters should be constrained to the users choice (like upper or lower asymptote), a constrained version of the Levenberg-Marquardt solver can be used (LevenbergMarquardtConstrained)! Accordingly, minimal and maximal parameter vectors must be provided.

open System
open FSharp.Stats
open FSharp.Stats.Fitting.NonLinearRegression
open FSharp.Stats.Fitting.LinearRegression

let time = [|0. .. 0.5 .. 8.|]

let cellCount =
    [|
    17000000.;16500000.;11000000.;14000000.;27000000.;40000000.;120000000.;
    300000000.;450000000.;1200000000.;2700000000.;5000000000.;
    8000000000.;11700000000.;12000000000.;13000000000.;12800000000.
    |]

let cellCountLn = cellCount |> Array.map log

open Plotly.NET

let chartOrig = 
    Chart.Point(time,cellCount)
    |> Chart.withTraceInfo "original data"
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withYAxisStyle "cells/ml"

let chartLog =
    Chart.Point(time,cellCountLn)
    |> Chart.withTraceInfo "log count"
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    
let growthChart = 
    [chartOrig;chartLog] |> Chart.Grid(2,1)

Manual phase selection

If growth phases are labelled manually, the exponential phase can be fitted with a regression line.

To determine the generation time, it is necessary to find the time interval it takes to double the count data. When a log₂ transform is used, a doubling of the original counts is achieved, when the log value moves 1 unit. Keeping that in mind, the slope can be used to calculate the time it takes for the log₂ data to increase 1 unit.

• slope * generation time = 1
• generation time = 1/slope

If a different log transform was used, the correction factor for the numerator is log_x(2).

// The exponential phase was defined to be between time point 1.5 and 5.5.
let logPhaseX = vector time.[3..11]
let logPhaseY = vector cellCountLn.[3..11]

// regression coefficients as [intercept;slope]
let regressionCoeffs =
    OLS.Linear.Univariable.fit logPhaseX logPhaseY

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

// The generation time is calculated by dividing log_x 2. by the regression line slope. 
// The log transform must match the used data transform. 
let slope = regressionCoeffs.[1]
let generationTime = log(2.) / slope


let fittedValues = 
    let f = OLS.Linear.Univariable.predict (Coefficients (vector [14.03859475; 1.515073487]))
    logPhaseX |> Seq.map (fun x -> x,f x)

let chartLinearRegression =
    [
    Chart.Point(time,cellCountLn)   |> Chart.withTraceInfo "log counts"
    Chart.Line(fittedValues)        |> Chart.withTraceInfo "fit"
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"

let generationTimeManual = sprintf "The generation time (manual selection) is: %.1f min" ((log(2.)/1.5150)* 60.)

generationTimeManual

Gompertz model

In the following example the four parameter gompertz function is applied to cell count data (Gibson et al., 1988).

The Gompertz model is fitted using the Levenberg Marquardt solver. Initial parameters are estimated from the original data. The expected generation time has to be approximated as initial guess.

For parameter interpretation the applied log transform is important and must be provided. If other parameters than cell count (e.g. size or length) should be analyzed, use id as value transform.

Gompertz parameters:

• A: lower asymptote
• B: relative growth rate (approximated by generation time consideration)
• C: upper asymptote - lower asymptote
• M: time point of inflection (maximal growth rate)

// The Levenberg Marquardt algorithm identifies the parameters that leads to the best fit 
// of the gompertz models to the count data. The solver must be provided with initial parameters
// that are estimated in the following:
let solverOptions (xData :float []) (yDataLog :float []) expectedGenerationTime (usedLogTransform: float -> float) =
    // lower asymptote
    let a = Seq.min yDataLog
    // upper asymptote - lower asymptote (y range)
    let c = (Seq.max yDataLog) - a
    // relative growth rate
    let b = usedLogTransform 2. * Math.E / (expectedGenerationTime * c)
    // time point of inflection (in gompertz model at f(x)=36% of the y range)
    let m = 
        let yAtInflection = a + c * 0.36
        Seq.zip xData yDataLog
        |> Seq.minBy (fun (xValue,yValue) ->
            Math.Abs (yValue - yAtInflection)
        )
        |> fst
    createSolverOption 0.001 0.001 10000 [|a;b;c;m|]

// By solving the nonlinear fitting problem, the optimal model parameters are determined
let gompertzParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.gompertz
        (solverOptions time cellCountLn 1. log)
        0.1
        10.
        time
        cellCountLn

let fittingFunction = 
    Table.GrowthModels.gompertz.GetFunctionValue gompertzParams

    
let fittedValuesGompertz =
    // The parameter were determined locally for saving time during build processes
    //let f = Table.GrowthModels.gompertz.GetFunctionValue (vector [|16.46850199; 0.7014917539; 7.274139441; 3.3947717|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,fittingFunction x
        ) 
    |> Chart.Line
    |> Chart.withTraceInfo "gompertz"

let fittedChartGompertz = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedValuesGompertz
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"

Generation time calculation

The generation time can be calculated by dividing log(2) by the slope of the inflection point. The used log transform must match the used log transform applied to the count data.

The four parameter Gompertz model allows the determination of generation times from its parameters (Gibson et al., 1988).

let generationtime (parametervector:Vector<float>) (logTransform:float -> float) =
    logTransform 2. * Math.E / (parametervector.[1] * parametervector.[2])

let lag (parametervector:Vector<float>) =
    (parametervector.[3] - 1.) / parametervector.[1]

let g = sprintf "The generation time (Gompertz) is: %.1f min" (60. * (generationtime gompertzParams log))
let l = sprintf "The lag phase duration is %.2f h" (lag gompertzParams)

"The generation time (Gompertz) is: 22.2 min"

"The lag phase duration is 3.41 h"

Other models

In the following other growth models are applied to the given data set:

• Richards
• Weibull
• Janoschek
• Exponential
• Verhulst
• Morgan-Mercer-Flodin
• von Bertalanffy

To determine the generation time, the slope at the inflection point must be calculated. As explained above, the generation time can be calculated by: logx(2)/(slope at inflection) where x is the used log transform.

Choose a appropriate growth model according to your needs.

For an overview please scroll down to see a combined diagram of all growth models.

Richards curve

Parameters:

• l: upper asymptote
• k: growth rate
• y: inflection point (x value)
• d: influences the inflection point on the y axis

let richardsParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.richards
        (createSolverOption 0.001 0.001 10000 [|23.;1.;3.4;2.|])
        0.1
        10.
        time
        cellCountLn

let fittingFunctionRichards = 
    Table.GrowthModels.richards.GetFunctionValue richardsParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeRichards (richardParameters:Vector<float>) =
    let l = richardParameters.[0]
    let k = richardParameters.[1]
    let y = richardParameters.[2] //x value of inflection point
    let d = richardParameters.[3]
    let gradientFunctionRichards t =
        (k*l*((d-1.)*Math.Exp(-k*(t-y))+1.)**(1./(1.-d)))/(Math.Exp(k*(t-y))+d-1.)
    let maximalSlope =
        gradientFunctionRichards y
    log(2.) / maximalSlope

let fittedValuesRichards =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.richards.GetFunctionValue (vector [|23.25211263; 7.053516315; 5.646889803; 111.0132522|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartRichards = 
    fittedValuesRichards
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTraceInfo "richards"

let fittedChartRichardsS = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedValuesRichards
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "richards"

let generationRichards = sprintf "The generation time (Richards) is: %.1f min" (generationtimeRichards (vector [|23.25211263; 7.053516315; 5.646889803; 111.0132522|]) * 60.)

"The generation time (Richards) is: 29.4 min"

Weibull

Parameters:

• b: lower asymptote
• l: upper asymptote
• k: growth rate
• d: influences the inflection point position

let weibullParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.weibull
        (createSolverOption 0.001 0.001 10000 [|15.;25.;1.;5.|])
        0.1
        10.
        time
        cellCountLn

let fittingFunctionWeibull = 
    Table.GrowthModels.weibull.GetFunctionValue weibullParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeWeibull (weibullParameters:Vector<float>) =
    let b = weibullParameters.[0]
    let l = weibullParameters.[1]
    let k = weibullParameters.[2]
    let d = weibullParameters.[3]
    let gradientFunctionWeibull t =
        (d*(l-b)*(k*t)**d*Math.Exp(-((k*t)**d)))/t
    let inflectionPointXValue =
        (1./k)*((d-1.)/d)**(1./d)
    let maximalSlope =
        gradientFunctionWeibull inflectionPointXValue
    log(2.) / maximalSlope

let fittedValuesWeibull =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.weibull.GetFunctionValue (vector [|16.40632433; 23.35537293; 0.2277752116; 2.900806071|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartWeibull = 
    fittedValuesWeibull
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTraceInfo "weibull"

let fittedChartWeibullS = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedValuesWeibull
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "weibull"

let generationWeibull = 
    sprintf "The generation time (Weibull) is: %.1f min" (generationtimeWeibull (vector [|16.40632433; 23.35537293; 0.2277752116; 2.900806071|]) * 60.)   

"The generation time (Weibull) is: 23.0 min"

Janoschek

Parameters:

• b: lower asymptote
• l: upper asymptote
• k: growth rate
• d: influences the inflection point position on the x axis

let janoschekParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.janoschek
        (createSolverOption 0.001 0.001 10000 [|15.;25.;1.;5.|])
        0.1
        10.
        time
        cellCountLn

let fittingFunctionJanoschek = 
    Table.GrowthModels.janoschek.GetFunctionValue janoschekParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeJanoschek (janoschekParameters:Vector<float>) =
    let b = janoschekParameters.[0]
    let l = janoschekParameters.[1]
    let k = janoschekParameters.[2]
    let d = janoschekParameters.[3]
    let gradientFunctionJanoschek t =
        d*k*(l-b)*t**(d-1.)*Math.Exp(-k*t**d)
    //Chart to estimate point of maximal slope (inflection point)
    let slopeChart() =
        [time.[0] .. 0.1 .. 8.] |> List.map (fun x -> x, gradientFunctionJanoschek x) |> Chart.Line
    let inflectionPointXValue =
        3.795
    let maximalSlope =
        gradientFunctionJanoschek inflectionPointXValue
    log(2.) / maximalSlope
    
let fittedValuesJanoschek =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.janoschek.GetFunctionValue (vector [|16.40633962; 23.35535182; 0.01368422994; 2.900857027|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartJanoschek = 
    fittedValuesJanoschek
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTraceInfo "janoschek"

let fittedChartJanoschekS = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedChartJanoschek
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "janoschek"

let generationJanoschek = 
    sprintf "The generation time (Janoschek) is: %.1f min" (generationtimeJanoschek (vector [|16.40633962; 23.35535182; 0.01368422994; 2.900857027|]) * 60.)

"The generation time (Janoschek) is: 23.0 min"

Exponential

The exponential model of course can not be applied to the lag phase.

Parameters:

• b: lower asymptote
• l: upper asymptote
• k: growth rate

let exponentialParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.exponential
        (createSolverOption 0.001 0.001 10000 [|15.;25.;0.5|])
        0.1
        10.
        time.[6..]
        cellCountLn.[6..]

let fittingFunctionExponential = 
    Table.GrowthModels.exponential.GetFunctionValue exponentialParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeExponential (expParameters:Vector<float>) =
    let b = expParameters.[0]
    let l = expParameters.[1]
    let k = expParameters.[2]
    let gradientFunctionExponential t =
        k*(l-b)*Math.Exp(-k*t)
    let maximalSlope =
        gradientFunctionExponential time.[6]
    log(2.) / maximalSlope

let fittedValuesExp =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.exponential.GetFunctionValue (vector [|4.813988967; 24.39950361; 0.3939132175|])
    [3.0 .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartExp = 
    fittedValuesExp
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTraceInfo "exponential"

let fittedChartExpS = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedChartExp
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "exponential"

let generationExponential = 
    sprintf "The generation time (Exp) is: %.1f min" (generationtimeExponential (vector [|4.813988967; 24.39950361; 0.3939132175|]) * 60.)
    

"The generation time (Exp) is: 17.6 min"

Verhulst

The verhulst growth model is a logistic function with a lower asymptote fixed at y=0. A 4 parameter version allows the lower asymptote to vary from 0.

Note: symmetric with inflection point at 50 % of y axis range

Parameters:

• l: upper asymptote
• k: x value at inflection point
• d: steepness
• b: lower asymptote

To apply the 3 parameter verhulst model with a fixed lower asymptote = 0 use the 'verhulst' model instead of 'verhulst4Param'.

let verhulstParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.verhulst4Param
        (createSolverOption 0.001 0.001 10000 [|25.;3.5;1.;15.|])
        0.1
        10.
        time
        cellCountLn

let fittingFunctionVerhulst() = 
    Table.GrowthModels.verhulst.GetFunctionValue verhulstParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeVerhulst (verhulstParameters:Vector<float>) =
    let lmax = verhulstParameters.[0]
    let k    = verhulstParameters.[1]
    let d    = verhulstParameters.[2]
    let lmin = verhulstParameters.[3]
    let gradientFunctionVerhulst t =
        ((lmax-lmin)*Math.Exp((k-t)/d))/(d*(Math.Exp((k-t)/d)+1.)**2.)
    let maximalSlope =
        gradientFunctionVerhulst k
    log(2.) / maximalSlope

let fittedValuesVerhulst =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.verhulst4Param.GetFunctionValue (vector [|23.39504328; 3.577488116; 1.072136278; 15.77380824|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartVerhulst = 
    fittedValuesVerhulst
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTraceInfo "verhulst"

let fittedChartVerhulstS = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedChartVerhulst
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "verhulst"

let generationVerhulst = 
    sprintf "The generation time (Verhulst) is: %.1f min" (generationtimeVerhulst (vector [|23.39504328; 3.577488116; 1.072136278; 15.77380824|]) * 60.)

"The generation time (Verhulst) is: 23.4 min"

Morgan-Mercer-Flodin

Parameters:

• b: count at t0
• l: upper asymptote
• k: growth rate
• d: influences the inflection point position

let morganMercerFlodinParams =
    LevenbergMarquardt.estimatedParams
        Table.GrowthModels.morganMercerFlodin
        (createSolverOption 0.001 0.001 10000 [|15.;25.;0.2;3.|])
        0.1
        10.
        time
        cellCountLn

let fittingFunctionMMF() = 
    Table.GrowthModels.morganMercerFlodin.GetFunctionValue morganMercerFlodinParams

Here is a pre-evaluated version (to save time during the build process, as the solver takes quite some time.)

let generationtimeMmf (mmfParameters:Vector<float>) =
    let b = mmfParameters.[0]
    let l = mmfParameters.[1]
    let k = mmfParameters.[2]
    let d = mmfParameters.[3]
    let gradientFunctionMmf t =
        (d*(l-b)*(k*t)**d)/(t*((k*t)**d+1.)**2.)
    //Chart to estimate point of maximal slope (inflection point)
    let slopeChart() =
        [time.[0] .. 0.1 .. 8.] |> List.map (fun x -> x, gradientFunctionMmf x) |> Chart.Line
    let inflectionPointXValue =
        3.45
    let maximalSlope =
        gradientFunctionMmf inflectionPointXValue
    log(2.) / maximalSlope

let generationMmf = 
    sprintf "The generation time (MMF) is: %.1f min" (generationtimeMmf (vector [|16.46099291; 24.00147463; 0.2500698772; 3.741048641|]) * 60.)

let fittedValuesMMF =
    // The parameter were determined locally for saving time during build processes
    let f =  Table.GrowthModels.morganMercerFlodin.GetFunctionValue (vector [|16.46099291; 24.00147463; 0.2500698772; 3.741048641|])
    [time.[0] .. 0.1 .. Seq.last time]
    |> Seq.map (fun x -> 
        x,f x
        ) 
    |> Chart.Line

let fittedChartMMF = 
    [
        Chart.Point(time,cellCountLn)
        |> Chart.withTraceInfo "log count"
        fittedValuesMMF |> Chart.withTraceInfo "morganMercerFlodin"
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"
    |> Chart.withTitle "morganMercerFlodin"

"The generation time (MMF) is: 21.9 min"

von Bertalanffy

Since this model expects a x axis crossing of the data it cannot be applied to the given data.

Parameters:

• l: upper asymptote
• k: growth rate
• t0: x axis crossing

Comparison between all models

Fit function

let combinedGrowthChart =
    [
        
        Chart.Point(time,cellCountLn) |> Chart.withTraceInfo "log count"
        Chart.Line(fittedValues)|> Chart.withTraceInfo "regression line"
        fittedValuesGompertz    |> Chart.withTraceInfo "Gompertz"
        fittedValuesRichards    |> Chart.withTraceInfo "Richards"
        fittedValuesWeibull     |> Chart.withTraceInfo "Weibull"
        fittedValuesJanoschek   |> Chart.withTraceInfo "Janoschek"
        fittedValuesExp         |> Chart.withTraceInfo "Exponential"
        fittedValuesVerhulst    |> Chart.withTraceInfo "Verhulst"
        fittedValuesMMF         |> Chart.withTraceInfo "MorganMercerFlodin"
    ]
    |> Chart.combine
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "time (h)"
    |> Chart.withYAxisStyle "ln(cells/ml)"

Generation time

let generationTimeTable =
    let header = ["<b>Model</b>";"<b>Generation time (min)"]
    let rows = 
        [
            ["manual selection (regression line)";      sprintf "%.1f" ((log(2.)/1.5150)* 60.)]    
            ["Gompertz";    sprintf "%.1f" (60. * (generationtime gompertzParams log))]    
            ["Richards";    sprintf "%.1f" (generationtimeRichards (vector [|23.25211263; 7.053516315; 5.646889803; 111.0132522|]) * 60.)]       
            ["Weibull";     sprintf "%.1f" (generationtimeWeibull (vector [|16.40632433; 23.35537293; 0.2277752116; 2.900806071|]) * 60.)  ]       
            ["Janoschek";   sprintf "%.1f" (generationtimeJanoschek (vector [|16.40633962; 23.35535182; 0.01368422994; 2.900857027|]) * 60.)]    
            ["Exponential"; sprintf "%.1f" (generationtimeExponential (vector [|4.813988967; 24.39950361; 0.3939132175|]) * 60.)]
            ["Verhulst";    sprintf "%.1f" (generationtimeVerhulst (vector [|23.39504328; 3.577488116; 1.072136278; 15.77380824|]) * 60.)] 
            ["MMF";         sprintf "%.1f" (generationtimeMmf (vector [|16.46099291; 24.00147463; 0.2500698772; 3.741048641|]) * 60.)] 
        ]
    
    Chart.Table(
        header, 
        rows,
        HeaderFillColor = Color.fromHex "#45546a",
        CellsFillColor = Color.fromColors [Color.fromHex "#deebf7";Color.fromString "lightgrey"]
        )

Model examples