Multiple testing correction: q values¶

TLDR: A q value defines the proportion of false positives there are within all discoveries that were called significant up to the current item.

Getting started: Multiple testing problem¶

High throughput techniques like microarrays with its successor RNA-Seq and mass spectrometry proteomics lead to an huge data amount. Thousands of features (e.g. transcripts or proteins) are measured simultaneously. Differential expression analysis aims to identify features, that change significantly between two conditions. A common experimental setup is the analysis of which genes are over- or underexpressed between e.g. a wild type and a mutant.

Hypothesis tests aim to identify differences between two or more samples. The most common statistical test is the t test that tests a difference of means. Hypothesis tests report a p value, that correspond the probability of obtaining results at least as extreme as the observed results, assuming that the null hypothesis is correct. In other words:

If there is no effect (no mean difference), a p value of 0.05 indicates that in 5 % of the tests a false positive is reported.

Referencing packages¶

Consider two population distributions that follow a normal distribution. Both have the same mean and standard deviation.

Samples with sample size 5 are randomly drawn from both population distributions. Both samples are tested if a mean difference exist using a two sample t test where equal variances of the underlying population distribution are assumed.

10,000 tests are performed, each with new randomly drawn samples. This corresponds to an experiment in which none of the features changed. Note, that the mean intensities are arbitrary and must not be the same for all features! In the presented case all feature intensities are in average 10. The same simulation can be performed with pairwise comparisons from distributions that differ for each feature, but are the same within the feature. The resulting p values are uniformly distributed between 0 and 1.

Fig 1: p value distribution of the null hypothesis.

Click me to see null hypothesis p value histogram code

let nullDist = 
   Array.init 10000 (fun x -> 
       let sA = getSample 5 distributionA
       let sB = getSample 5 distributionB
       (Testing.TTest.twoSample true sA sB).PValue
       )


let nullDistributionChart = 
    nullDist 
    |> Distributions.Frequency.create 0.025 
    |> Map.toArray 
    |> Array.map (fun (k,c) -> k,float c) 
    |> Chart.StackedColumn 
    |> Chart.withTraceInfo "alt"
    |> Chart.withTemplate ChartTemplates.lightMirrored
    |> Chart.withXAxisStyle "pvalue"
    |> Chart.withYAxisStyle "frequency"

let thresholdLine =
    Shape.init(ShapeType=ShapeType.Line,X0=0.05,X1=0.05,Y0=0.,Y1=300.)

nullDistributionChart

Samples are called significantly different, if their p value is below a certain significance threshold ($\alpha$ level). While "the lower the better", a common threshold is a p value of 0.05 or 0.01. In the presented case in average $10,000 * 0.05 = 500$ tests are significant (red box), even though the populations do not differ. They are called false positives (FP). Now lets repeat the same experiment, but this time sample 70% of the time from null features (no difference) and add 30% samples of truly differing distributions. Therefore a third populations is generated, that differ in mean, but has an equal standard deviation:

Fig 2: p value distribution of the alternative hypothesis. Blue coloring indicate p values deriving from distribution A and B (null). Orange coloring indicate p values deriving from distribution A and C (truly differing).

The pvalue distribution of the tests resulting from truly differing populations are right skewed, while the null tests again show a homogeneous distribution between 0 and 1. Many, but not all of the tests that come from the truly differing populations are below 0.05, and therefore would be reported as significant. In average 350 null features would be reported as significant even though they derive from null features (blue bars, 10,000 x 0.7 x 0.05 = 350).

The multiple testing problem¶

The hypothesis testing framework with the p value definition given above was developed for performing just one test. If many tests are performed, like in modern high throughput studies, the probability to obtain a false positive result increases. The probability of at least one false positive is called Familywise error rate (FWER) and can be determined by $FWER=1-(1-\alpha)^m$ where $\alpha$ corresponds to the significance threshold (here 0.05) and $m$ is the number of performed tests.

Fig 3: Family wise error rate depending on number of performed tests. The black dashed line indicates the Bonferroni corrected FWER by $p^* = \frac{\alpha}{m}$ .

When 10,000 null features are tested with a p value threshold of 0.05, in average 500 tests are reported significant even if there is not a single comparisons in which the population differ. If some of the features are in fact different, the number of false positives consequently decreases (remember, the p value is defined for tests of null features).

Why the interpretation of high throughput data based on p values is difficult: The more features are measured, the more false positives you can expect. If 100 differentially expressed genes are identified by p value thresholding, without further information about the magnitude of expected changes and the total number of measured transcripts, the data is useless.

The p value threshold has no straight-forward interpretation when many tests are performed. Of course you could restrict the family wise error rate to 0.05, regardless how many tests are performed. This is realized by dividing the $\alpha$ significance threshold by the number of tests, which is known as Bonferroni correction: $p^* = \frac{\alpha}{m}$. This correction drastically limit the false positive rate, but in an experiment with a huge count of expected changes, it additionally would result in many false negatives. The FWER should be chosen if the costs of follow up studies to tests the candidates are dramatic or there is a huge waste of time to potentially study false positives.

False discovery rate¶

A more reasonable measure of significance with a simple interpretation is the so called false discovery rate (FDR). It describes the rate of expected false positives within the overall reported significant features. The goal is to identify as many sig. features as possible while incurring a relatively low proportion of false positives. Consequently a set of reported significant features together with the FDR describes the confidence of this set, without the requirement to somehow incorporate the uncertainty that is introduced by the total number of tests performed. In the simulated case of 7,000 null tests and 3,000 tests resulting from truly differing distributions above, the FDR can be calculated exactly. Therefore at e.g. a p value of 0.05 the number of false positives (blue in red box) are divided by the number of significant reported tests (false positives + true positives).

Fig 4: p value distribution of the alternative hypothesis.

Given the conditions described in the first chapter, the FDR of this experiment with a p value threshold of 0.05 is 0.173. Out of the 2019 reported significant comparisons, in average 350 are expected to be false positives, which gives an straight forward interpretation of the data confidence. In real-world experiments the proportion of null tests and tests deriving from an actual difference is of course unknown. The proportion of null tests however tends to be distributed equally in the p value histogram. By identification of the average null frequency, a proportion of FP and TP can be determined and the FDR can be defined. This frequency estimate is called $\pi_0$, which leads to an FDR definition of:

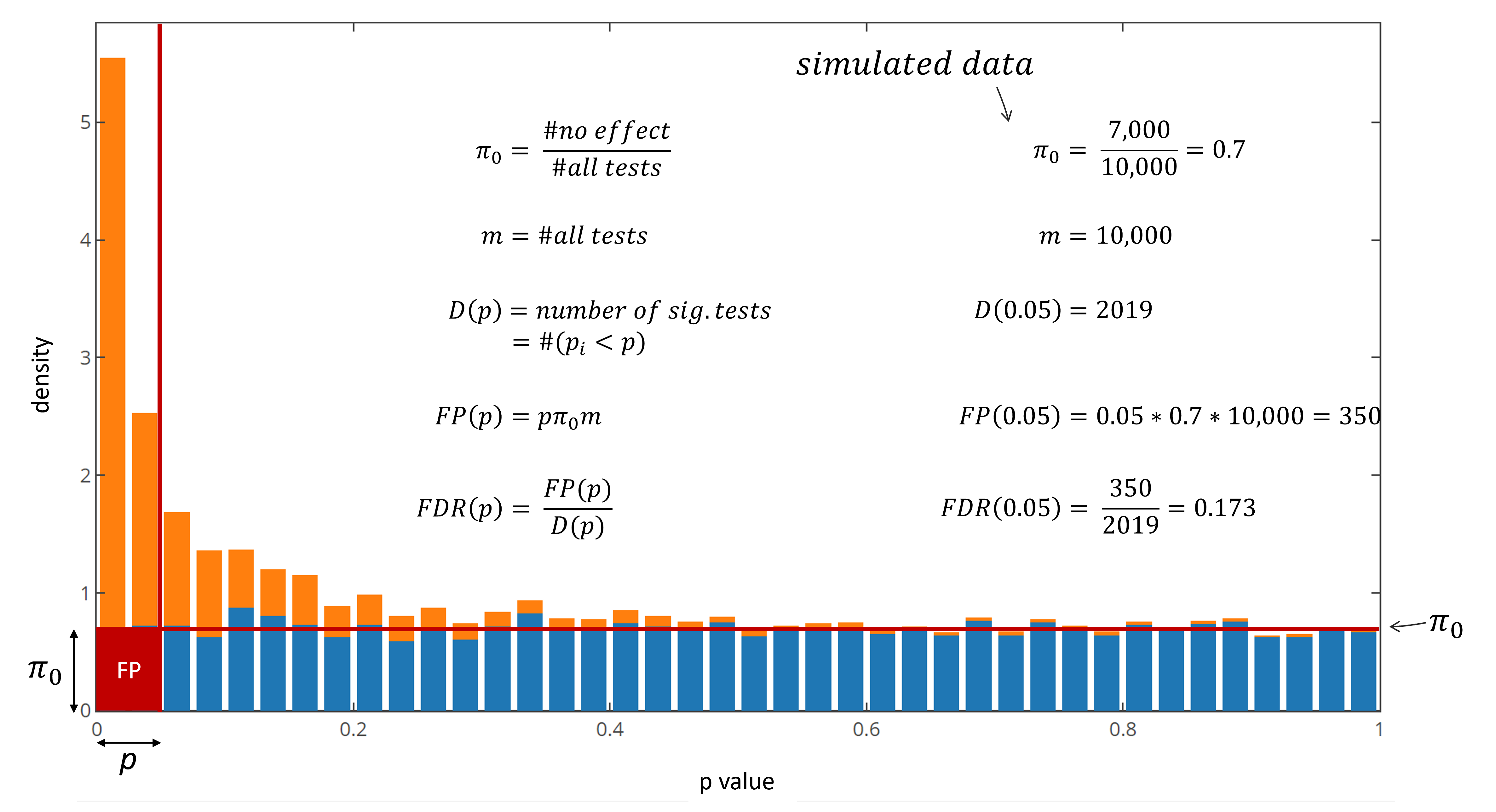
Fig 5: FDR calculation on simulated data.

q value¶

Consequently for each presented p value a corresponding FDR can be calculated. The minimum local FDR at each p value is called q value.

$$\hat q(p_i) = min_{t \geq p_i} \hat{FDR}(p_i)$$

Since the q value is not monotonically increasing, it is smoothed by assigning the lowest FDR of all p values, that are equal or higher the current one.

By defining $\pi_0$, all other parameters can be calculated from the given p value distribution to determine the all q values. The most prominent FDR-controlling method is known as Benjamini-Hochberg correction. It sets $\pi_0$ as 1, assuming that all features are null. In studies with an expected high proportion of true positives, a $\pi_0$ of 1 is too conservative, since there definitely are true positives in the data.

A better estimation of $\pi_0$ is given in the following:

True positives are assumed to be right skewed while null tests are distributed equally between 0 and 1. Consequently the right flat region of the p value histogram tends to correspond to the true frequency of null comparisons (Fig 5). As real world example 9856 genes were measured in triplicates under two conditions (control and treatment). The p value distribution of two sample t tests looks as follows:

Fig 6: p value distributions of real world example. The frequency is given on the right, its density on the left. The black dashed line indicates the distribution, if all features were null. The red dash-dotted line indicates the visual estimated pi0.

By performing t tests for all comparisons 3743 (38 %) of the genes lead to a pvalue lower than 0.05. By eye, you would estimate $\pi_0$ as 0.4, indicating, only a small fraction of the genes are unaltered (null). After q value calculations, you would filter for a specific FDR (e.g. 0.05) and end up with an p value threshold of 0.04613, indicating a FDR of max. 0.05 in the final reported 3642 genes.

pi0     = 0.4
m       = 9856
D(p)    = number of sig. tests at given p
FP(p)   = p*0.4*9856
FDR(p)  = FP(p) / D(p)

FDR(0.04613) = 0.4995

Now let's compare p- to its corresponding q values with ensuring continuity

Fig 7: FDR calculation on experiment data. Please zoom into the very first part of the curve to inspect the monotonicity.

The automatic detection of $\pi_0$ is facilitated as follows¶

For a range of $\lambda$ in e.g. $\{0.0 .. 0.05 .. 0.95\}$, calculate $\hat \pi_0 (\lambda) = \frac {\#[p_j > \lambda]}{m(1 - \lambda)}$

Fig 8: pi0 estimation.

The resulting diagram shows, that with increasing $\lambda$ its function value $\hat \pi_0(\lambda)$ tends to $\pi_0$. The calculation relates the actual proportion of tests greater than $\lambda$ to the proportion of $\lambda$ range the corresponding p values are in. In Storey & Tibshirani 2003 this curve is fitted with a cubic spline. A weighting of the knots by $(1 - \lambda)$ is recommended but not specified in the final publication. Afterwards the function value at $\hat \pi_0(1)$ is defined as final estimator of $\pi_0$. This is often referred to as the smoother method.

Another method (bootstrap method) (Storey et al., 2004), that does not depend on fitting is based on bootstrapping and was introduced in Storey et al. (2004). It is implemented in FSharp.Stats:

1. Determine the minimal $\hat \pi_0 (\lambda)$ and call it $min \hat \pi_0$ .

2. For each $\lambda$, bootstrap the p values (e.g. 100 times) and calculate the mean squared error (MSE) from the difference of resulting $\hat \pi_0^b$ to $min \hat \pi_0$. The minimal MSE indicates the best $\lambda$. With $\lambda$

defined, $\pi_0$ can be determined. Note: When bootstrapping an data set of size n, n elements are drawn with replacement.

Fig 9: Bootstrapping for pi0 estimation. The dashed line indicates the minimal pi0 from Fig. 8. The bootstrapped pi0 distribution that shows the least variation to the dashed line is the optimal. In the presented example it is either 0.8 or 0.85.

For an $\lambda$, range of $\{0.0 .. 0.05 .. 0.95\}$ the bootstrapping method determines either 0.8 or 0.85 as optimal $\lambda$ and therefore $optimal \hat \pi_0$ is either $0.3703$ or $0.3686$.

The automated estimation of $\pi_0$ based on bootstrapping is implemented in FSharp.Stats.Testing.MultipleTesting.Qvalues.

Subsequent to $\pi_0$ estimation the q values can be determined from a list of p values.

Variants¶

A robust variant of q value determination exists, that is more conservative for small p values when the total number of p values is low. Here the number of false positives is divided by the number of total discoveries multiplied by the FWER at the current p value. The correction takes into account the probability of a false positive being reported in the first place.

Especially when the population distributions do not follow a perfect normal distribution or the p value distribution looks strange, the usage of the robust version is recommended.

$qval = {\#FP \over \#Discoveries}$

$qval_{robust} = {\#FP \over \#Discoveries \times (1-(1-p)^m)}$

Fig 10: Comparison of q values and robust q values, that is more conservative at low p values.

Quality plots¶

Fig 11: p value relation to q values. At a p value of 1 the q value is equal to pi0 (black dashed line).

Fig 12: p value density distribution. The dashed line indicates pi0 estimated by Storeys bootstrapping method.

Fig 13: Visual pi0 estimation.

Definitions and Notes¶

• Benjamini-Hochberg (BH) correction is equal to q values with $\pi_0 = 1$
• Storey & Tibshirani (2003):
  • "The 0.05 q-value cut-off is arbitrary, and we do not recommend that this value necessarily be used."
  • "The q-value for a particular feature is the expected proportion of false positives occurring up through that feature on the list."
  • "The precise definition of the q-value for a particular feature is the following. The q-value for a particular feature is the minimum false discovery rate that can be attained when calling all features up through that one on the list significant."
  • "The Benjamini & Hochberg (1995) methodology also forces one to choose an acceptable FDR level before any data are seen, which is often going to be impractical."
• To improve the q value estimation if the effects are asymmetric, meaning that negative effects are stronger than positives, or vice versa a method was published in 2014 by Orr et al.. They estimate a global $m_0$ and then split the p values

in two groups before calculating q values for each p value set. The applicability of this strategy however is questionable, as the number of up- and downregulated features must be equal, which is not the case in most biological experimental setups.

• The distinction of FDR and pFDR (positive FDR) is not crucial in the presented context, because in high throughput experiments with m>>100: Pr(R > 0) ~ 1 (Storey & Tibshirani, 2003, Appendix Remark A).
• The local FDR (lFDR) is sometimes referred to as the probability that for the current p value the null hypothesis is true (Storey 2011).
• If you have found typos, errors, or misleading statements, please feel free to file a pull request or contact me.

FAQ¶

• Why are q values lower than their associated p values?

  • q values are not necessarily greater than their associated p values. q values can maximal be pi0. The definition of p values is not the same as for q values! A q

  value defines what proportion of the reported discoveries may be false.

• Which cut off should I use?

  • "The 0.05 q-value cut-off is arbitrary, and we do not recommend that this value necessarily be used." (Storey 2003). It depends on your experimental design and the number of false positives you are willing to accept.

  If there are 20 discoveries, you may argue to accept if 2 of them are false positives (FDR=0.1). On the other hand, if there are 10,000 discoveries with 1,000 false positives (FDR=0.1) you may should reduce the FDR. Thereby the proportion of false positives decreases. Of course in this case the number of positives will decrease as well. It all breaks down to the matter of willingness to accept a certain number of false positives within your study. Studies, that aim to identify the presence of an specific protein of interest, the FDR should be kept low, because it inflates the risk, that this particular candidate is a false positive. If confirmatory follow up studies are cheap, you can increase the FDR, if they are expensive, you should restrict the number of false positives to avoid unpleasant discussions with your supervisor.

• In my study gene RBCM has an q value of 0.03. Does that indicate, there is a 3% chance, that it is an false positive?

  • No, actually the change that this particular gene is an false positive may actually be higher, because there may be genes that are much more significant than MSH2. The q value indicates,

  that 3% of the genes that are as or more extreme than RBCM are false positives (Storey 2003).

• Should I use the default or robust version for my study?

• When should I use q values over BH correction, or other multiple testing variants?

  • There is no straight forward answer to this question. If you are able to define a confident pi0 estimate by eye when inspecting the p value distribution, then the q value approach may be feasible.

  If you struggle in defining pi0, because the p value distribution has an odd shape or there are too few p values on which you base your estimate, it is better to choose the more conservative BH correction, or even consider other methodologies.

References¶

• Storey JD, Tibshirani R, Statistical significance for genomewide studies, 2003 DOI: 10.1073/pnas.1530509100
• Storey JD, Taylor JE, Siegmund D, Strong Control, Conservative Point Estimation and Simultaneous Conservative Consistency of False Discovery Rates: A Unified Approach, 2004, http://www.jstor.org/stable/3647634.
• Storey JD, Princeton University, 2011, preprint
• Orr M, Liu P, Nettleton D, An improved method for computing q-values when the distribution of effect sizes is asymmetric, 2014, doi: 10.1093/bioinformatics/btu432
• NettletonD et al., Estimating the Number of True Null Hypotheses from a Histogram of p Values., 2006, http://www.jstor.org/stable/27595607.
• Benjamini Y, Hochberg Y, On the Adaptive Control of the False Discovery Rate in Multiple Testing With Independent Statistics, 2000, doi:10.3102/10769986025001060