Clustering with FSharp.Stats I: k-means¶
Summary: This tutorial demonstrates k means clustering with FSharp.Stats and how to visualize the results with Plotly.NET.
Introduction¶
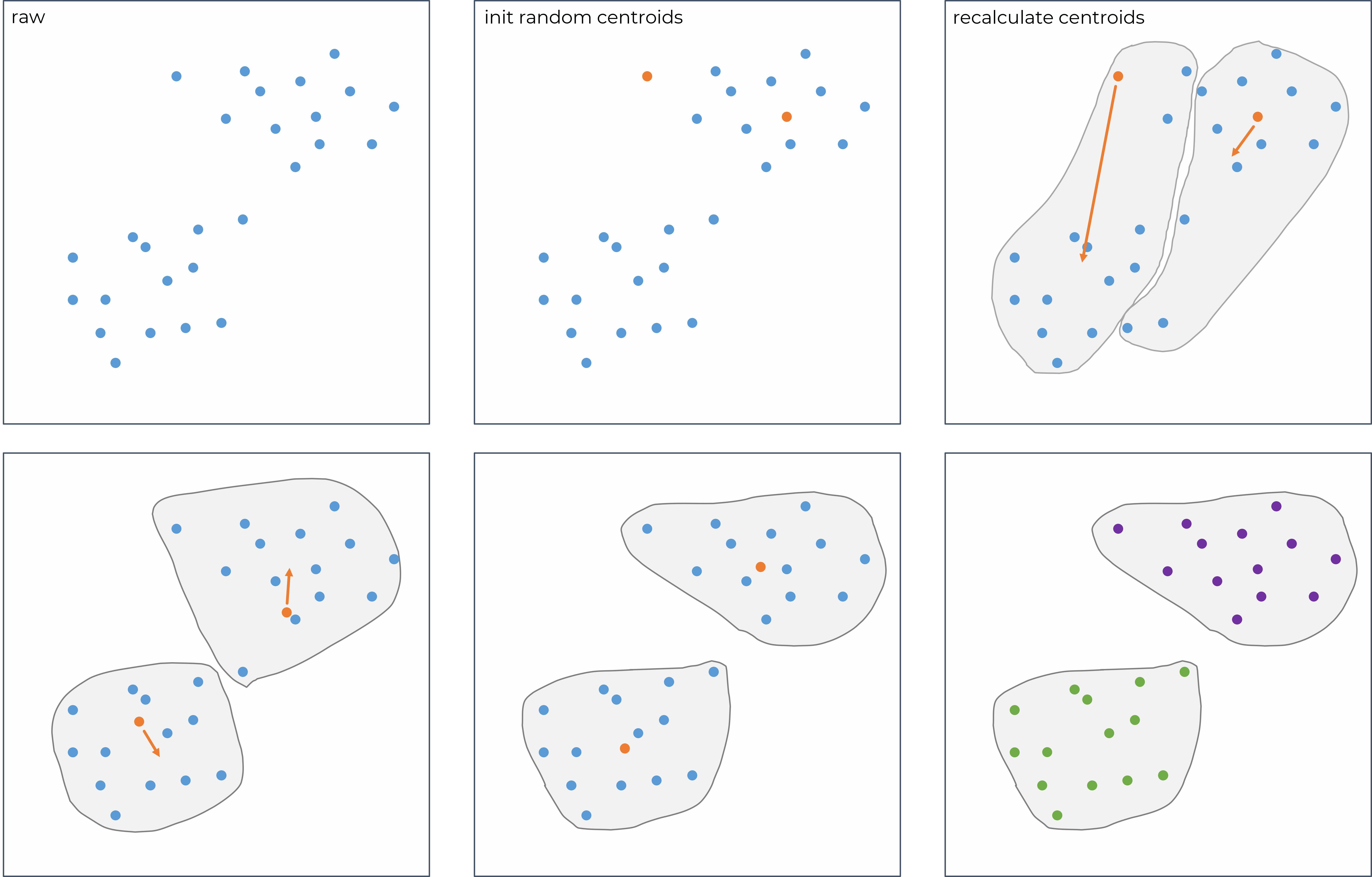
Clustering methods can be used to group elements of a huge data set based on their similarity. Elements sharing similar properties cluster together and can be reported as coherent group. k-means clustering is a frequently used technique, that segregates the given data into k clusters with similar elements grouped in each cluster, but high variation between the clusters. The algorithm to cluster a n-dimensional dataset can be fully described in the following 4 steps:
- Initialize k n-dimensional centroids, that are randomly distributed over the data range.
- Calculate the distance of each point to all centroids and assign it to the nearest one.
- Reposition all centroids by calculating the average point of each cluster.
- Repeat step 2-3 until convergence.
Centroid initiation¶
Since the random initiation of centroids may influences the result, a second initiation algorithm is proposed (cvmax), that extract a set of medians from the dimension with maximum variance to initialize the centroids.
Distance measure¶
While several distance metrics can be used (e.g. Manhattan distance or correlation measures) it is preferred to use Euclidean distance. It is recommended to use a squared Euclidean distance. To not calculate the square root does not change the result but saves computation time.
For demonstration of k-means clustering, the classic iris data set is used, which consists of 150 records, each of which contains four measurements and a species identifier.
Referencing packages¶
#r "nuget: Deedle.Interactive, 3.0.0"
#r "nuget: FSharp.Stats, 0.4.3"
#r "nuget: Plotly.NET.Interactive, 4.0.0"
#r "nuget: FSharp.Data, 4.2.7"
- Deedle.Interactive, 3.0.0
- FSharp.Data, 4.2.7
- FSharp.Stats, 0.4.3
- Plotly.NET.Interactive, 4.0.0
Loading data¶
open FSharp.Data
open Deedle
// Retrieve data using the FSharp.Data package and read it as dataframe using the Deedle package
let rawData = Http.RequestString @"https://raw.githubusercontent.com/fslaborg/datasets/main/data/iris.csv"
let df = Frame.ReadCsvString(rawData)
df
| sepal_length | sepal_width | petal_length | petal_width | species | (Decimal) | (Decimal) | (Decimal) | (Decimal) | (string) |
|---|---|---|---|---|---|---|
| 0 | -> | 5.5 | 2.4 | 3.8 | 1.1 | versicolor |
| 1 | -> | 4.9 | 3.1 | 1.5 | 0.1 | setosa |
| 2 | -> | 7.6 | 3 | 6.6 | 2.1 | virginica |
| 3 | -> | 5.6 | 2.8 | 4.9 | 2 | virginica |
| 4 | -> | 6.1 | 3 | 4.9 | 1.8 | virginica |
| : | ... | ... | ... | ... | ... | |
| 145 | -> | 7.7 | 2.6 | 6.9 | 2.3 | virginica |
| 146 | -> | 5.7 | 2.6 | 3.5 | 1 | versicolor |
| 147 | -> | 5.9 | 3 | 5.1 | 1.8 | virginica |
| 148 | -> | 6.8 | 3.2 | 5.9 | 2.3 | virginica |
| 149 | -> | 5 | 3.6 | 1.4 | 0.2 | setosa |
150 rows x 5 columns
0 missing values
open Plotly.NET
let colNames = ["sepal_length";"sepal_width";"petal_length";"petal_width"]
// isolate data as float [] []
let data =
Frame.dropCol "species" df
|> Frame.toJaggedArray
//isolate labels as seq<string>
let labels =
Frame.getCol "species" df
|> Series.values
|> Seq.mapi (fun i s -> sprintf "%s_%i" s i)
Chart.Heatmap(data,colNames=colNames,rowNames=labels)
// required to fit the species identifier on the left side of the heatmap
|> Chart.withMarginSize(Left=100.)
|> Chart.withTitle "raw iris data"
Clustering¶
The function that performs k-means clustering can be found at FSharp.Stats.ML.Unsupervised.IterativeClustering.kmeans. It requires four input parameters:
- Centroid initiation method
- Distance measure (from
FSharp.Stats.ML.DistanceMetrics) - Data to cluster as
float [] [], where each entry of the outer array is a sequence of coordinates - k, the number of clusters that are desired
open FSharp.Stats
open FSharp.Stats.ML
open FSharp.Stats.ML.Unsupervised
// For random cluster initiation use randomInitFactory:
let rnd = System.Random()
let randomInitFactory : IterativeClustering.CentroidsFactory<float []> =
IterativeClustering.randomCentroids<float []> rnd
// For assisted cluster initiation use cvmaxFactory:
//let cvmaxFactory : IterativeClustering.CentroidsFactory<float []> =
// IterativeClustering.intitCVMAX
let distanceFunction = DistanceMetrics.euclideanNaNSquared
let kmeansResult =
IterativeClustering.kmeans distanceFunction randomInitFactory data 4
let clusteredIrisData =
Seq.zip labels data
|> Seq.map (fun (species,dataPoint) ->
let clusterIndex,centroid = kmeansResult.Classifier dataPoint
clusterIndex,species,dataPoint)
clusteredIrisData
|> Seq.take 7
|> Seq.map (fun (a,b,c) -> sprintf "%i, %A, %A" a b c)
|> String.concat "\n"
|> fun x -> x + "\n ... "
1, "versicolor_0", [|5.5; 2.4; 3.8; 1.1|] 4, "setosa_1", [|4.9; 3.1; 1.5; 0.1|] 2, "virginica_2", [|7.6; 3.0; 6.6; 2.1|] 1, "virginica_3", [|5.6; 2.8; 4.9; 2.0|] 1, "virginica_4", [|6.1; 3.0; 4.9; 1.8|] 2, "virginica_5", [|6.3; 3.4; 5.6; 2.4|] 1, "virginica_6", [|6.2; 2.8; 4.8; 1.8|] ...
Visualization of the clustering result as heatmap¶
The datapoints are sorted according to their associated cluster index and visualized in a combined heatmap.
open FSharpAux
clusteredIrisData
//sort all data points according to their assigned cluster number
|> Seq.sortBy (fun (clusterIndex,label,dataPoint) -> clusterIndex)
|> Seq.unzip3
|> fun (_,labels,d) ->
Chart.Heatmap(d,colNames=colNames,rowNames=labels)
// required to fit the species identifier on the left side of the heatmap
|> Chart.withMarginSize(Left=100.)
|> Chart.withTitle "clustered iris data (k-means clustering)"
To visualize the result in a three-dimensional chart, three of the four measurements are isolated after clustering and visualized as 3D-scatter plot.
//group clusters
clusteredIrisData
|> Seq.groupBy (fun (clusterIndex,label,dataPoint) -> clusterIndex)
//for each cluster generate a scatter plot
|> Seq.map (fun (clusterIndex,cluster) ->
cluster
|> Seq.unzip3
|> fun (clusterIndex,label,data) ->
let clusterName = sprintf "cluster %i" (Seq.head clusterIndex)
//for 3 dimensional representation isolate sepal length, petal length, and petal width
let truncData = data |> Seq.map (fun x -> x.[0],x.[2],x.[3])
Chart.Scatter3D(truncData,mode=StyleParam.Mode.Markers,Name = clusterName,MultiText=label)
)
|> Chart.combine
|> Chart.withTitle "isolated coordinates of clustered iris data (k-means clustering)"
|> Chart.withXAxisStyle colNames.[0]
|> Chart.withYAxisStyle colNames.[2]
|> Chart.withZAxisStyle colNames.[3]
Optimal cluster number¶
The identification of the optimal cluster number k in terms of the average squared distance of each point to its centroid can be realized by performing the clustering over a range of k's multiple times and taking the k according to the elbow criterion. Further more robust and advanced cluster number determination techniques can be found here.
let getBestkMeansClustering bootstraps k =
let dispersions =
Array.init bootstraps (fun _ ->
IterativeClustering.kmeans distanceFunction randomInitFactory data k
)
|> Array.map (fun clusteringResult -> IterativeClustering.DispersionOfClusterResult clusteringResult)
Seq.mean dispersions,Seq.stDev dispersions
let iterations = 10
let maximalK = 10
[2 .. maximalK]
|> List.map (fun k ->
let mean,stdev = getBestkMeansClustering iterations k
k,mean,stdev
)
|> List.unzip3
|> fun (ks,means,stdevs) ->
Chart.Line(ks,means)
|> Chart.withYErrorStyle(Array=stdevs)
|> Chart.withXAxisStyle "k"
|> Chart.withYAxisStyle "average dispersion"
|> Chart.withTitle "iris data set average dispersion per k"
Limitations¶
- Outlier have a strong influence on the positioning of the centroids.
- Determining the correct number of clusters in advance is critical. Often it is chosen according to the number of classes present in the dataset which isn't in the spirit of clustering procedures.
Notes¶
- Please note that depending on what data you want to cluster, a column wise z-score normalization may be required. In the presented example differences in sepal width have a reduced influence because the absolute variation is low.
References¶
- FSharp.Stats documentation, fslaborg, https://fslab.org/FSharp.Stats/Clustering.html
- Shraddha and Saganna, A Review On K-means Data Clustering Approach, International Journal of Information & Computation Technology, Vol:4 No:17, 2014
- Moth'd Belal, A New Algorithm for Cluster Initialization, International Journal of Computer and Information Engineering, Vol:1 No:4, 2007
- Singh et al., K-means with Three different Distance Metrics, International Journal of Computer Applications, 2013, DOI:10.5120/11430-6785
- Kodinariya and Makwana, Review on Determining of Cluster in K-means Clustering, International Journal of Advance Research in Computer Science and Management Studies, 2013
Further reading¶
Examples are taken from FSharp.Stats documentation that covers various techniques for an optimal cluster number determination.
The next article in this series covers hierarchical clustering using FSharp.Stats.