Pearson correlation coefficient, Correlation Matrices and Heatmap¶

Introduction:¶

In this Blogpost we want to explain what a correlation matrix is, how they work, how we create them, and how to interpret them. We will explain this procedure using a real RNA-Seq dataset. So lets get started.

What is a RNA-Seq?¶

RNA-Seq, an abbreviation for RNA sequencing, is a method that utilizes next-generation sequencing to identify and quantify RNA molecules in a biological sample. This technique offers a comprehensive view of gene expression within the sample, referred to as the transcriptome. RNA-Seq specifically allows for the analysis of alternative transcripts, post-transcriptional modifications, gene fusions, mutations and single nucleotide polymorphisms (SNPs), as well as variations in gene expression over time or differences in gene expression between distinct groups or treatments.

In addition to mRNA transcripts, the method can look at different populations of RNA, including:

total RNA
small RNA such as miRNA
tRNA
ribosomal profiling.

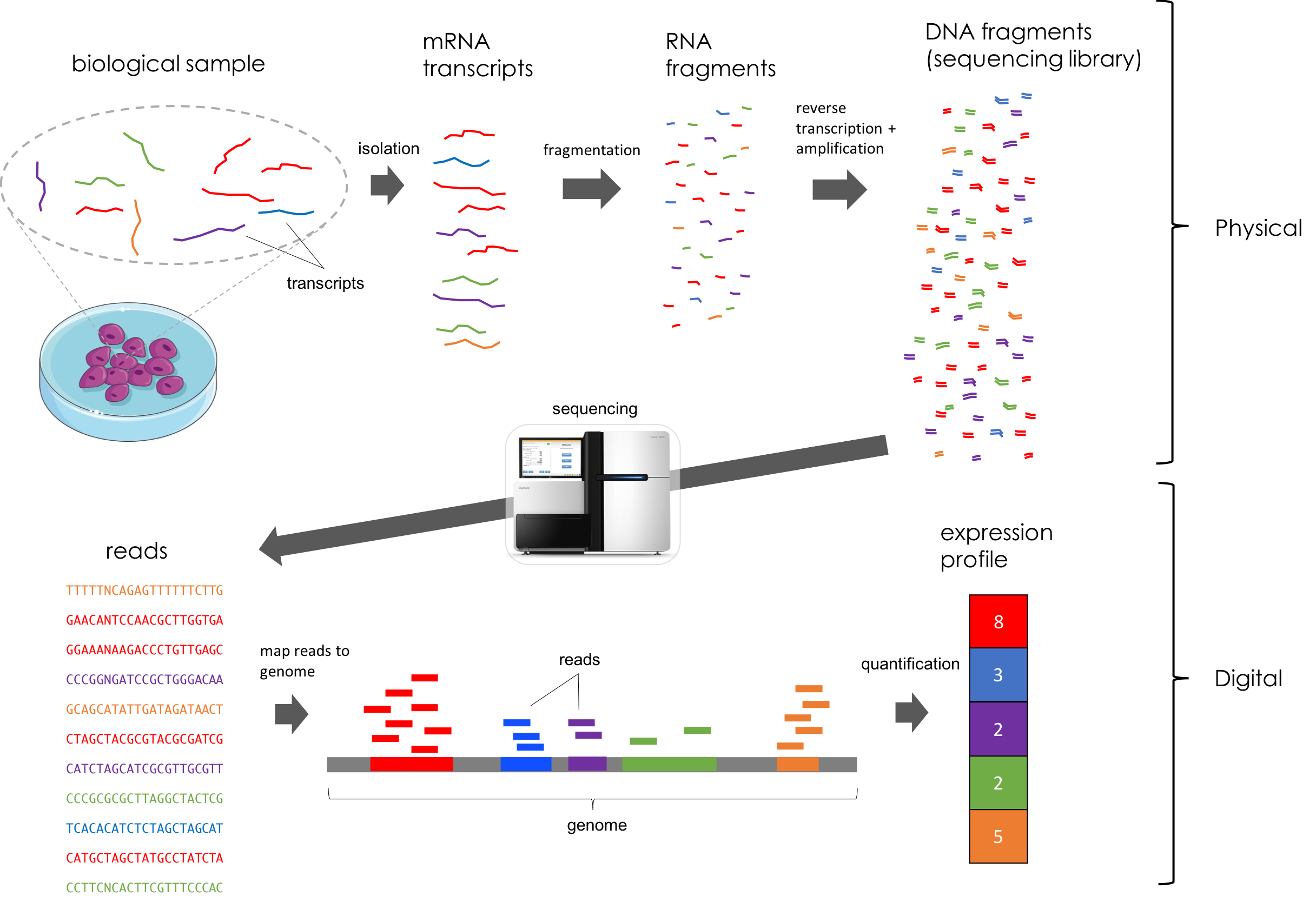
No description has been provided for this image

The Experiment¶

Our dataframe is based on an experiment that focused on cold acclimation in the model organism A. thaliana. The experiment was conducted to see if there are gene expression changes that are related to the influence of cold.

All the samples were grown for 4 days under the influence of the named coining condition (acclimation phase). After 4 days, all plants were shifted to the "control condition" (deacclimation phase). Three measurements were taken at each time point. This means that we are working with replicates here.

1 minute
15 minutes
180 minutes
1,5 Days
4 Days.

What we expect¶

What we generally expect is, that when the plant first comes into contact with the cold, the expression level of some genes changes, and then decreases over time. Other genes are always expressed at a constant level.

Here we compare replica groups at two different points in time, then calculate the Pearson correlation coefficient and create a heat map based on it. Here it is important to remember that we are not comparing individual genes, but two replica groups at a specific point in time. We expect our replica groups to differ in the various time intervals. The statistics we use here also serve as a quality measure for our experiment. So we cannot make any real biological statements here in relation to a different gene expression rate, only express how similar or dissimilar the replica groups are to each other.

Lets get ready to rumble:¶

At first intall the packages you need and open them:

In [ ]:

#r "nuget: Deedle.Interactive, 3.0.0"
#r "nuget: Plotly.NET, 4.2.0"
#r "nuget: Plotly.NET.Interactive, 4.2.1"
#r "nuget: FSharp.Stats.Interactive, 0.5.1-preview.2"
#r "nuget: BioFSharp, 2.0.0-preview.3"
#r "nuget: BioFSharp.IO, 2.0.0-preview.3"
#r "nuget: Deedle, 3.0.0"

In [2]:

open Deedle.Interactive
open Plotly.NET.Interactive
open FSharp.Stats.Interactive
open BioFSharp
open BioFSharp.IO
open Deedle
open FSharp.Stats
open FSharp.Stats.Signal.Outliers
open Plotly.NET

Start of the Journey¶

For the data we worked with a CSV file. For that we give the complete path. Additionally, we give the input how the CSV file is structured, consisting of headers and comma separators. For to make it easier to work with our dataframe, we induce an index using the respective genes

In [3]:

let basePath = __SOURCE_DIRECTORY__
let filePath = ("../notebooks/1/data/Cold.csv")
let data = Frame.ReadCsv (filePath, hasHeaders =true, separators = ",")

let indexedFrame : Frame<string, string> = 
    Frame.indexRows "Transcript" data 
indexedFrame

		Cold_t_1_r_1_d_FALSE	Cold_t_1_r_1_d_TRUE	Cold_t_1_r_2_d_FALSE	Cold_t_1_r_2_d_TRUE	Cold_t_15_r_1_d_FALSE	Cold_t_15_r_1_d_TRUE	Cold_t_15_r_2_d_FALSE	Cold_t_15_r_2_d_TRUE	Cold_t_15_r_3_d_FALSE	Cold_t_15_r_3_d_TRUE	...	Cold_t_2880_r_2_d_FALSE	Cold_t_2880_r_2_d_TRUE	Cold_t_2880_r_3_d_FALSE	Cold_t_2880_r_3_d_TRUE	Cold_t_5760_r_1_d_FALSE	Cold_t_5760_r_1_d_TRUE	Cold_t_5760_r_2_d_FALSE	Cold_t_5760_r_2_d_TRUE	Cold_t_5760_r_3_d_FALSE	Cold_t_5760_r_3_d_TRUE
		(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)	...	(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)	(int)
AT1G01010	->	13	18	15	45	21	18	13	43	12	40	...	32	8	51	18	41	15	43	20	36	9
AT1G01020	->	50	78	54	83	74	77	74	92	90	75	...	76	67	63	44	70	64	57	72	85	38
AT1G01030	->	30	34	26	34	23	26	23	32	42	26	...	21	21	37	33	26	26	22	24	29	17
AT1G01040	->	187	153	207	190	214	145	139	172	158	178	...	294	224	250	198	173	228	112	233	244	155
AT1G01050	->	242	275	224	332	242	278	268	437	215	386	...	394	197	358	174	332	221	262	208	313	128
:		...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
ATMG09980	->	17	12	12	17	18	11	5	20	6	10	...	29	11	30	3	15	5	13	12	6	2
ATMG01370	->	9	28	11	27	4	41	19	35	22	35	...	43	11	26	5	64	27	40	16	30	15
ATMG01390	->	248	676	331	374	362	314	391	480	1019	356	...	705	1054	406	223	1017	1158	776	484	455	555
ATMG01400	->	6	0	1	0	0	4	1	2	0	1	...	0	1	1	1	1	2	0	1	0	0
ATMG01410	->	7	14	20	29	18	36	11	28	26	19	...	23	6	29	8	29	24	33	22	23	5

18873 rows x 28 columns

0 missing values

Dataframe 2.0¶

You see we now have a cleaner dataframe but it is still massive. In this example we will only use six columns, the replicates for minute 15 and the replicates for 4 days. We use those time intervals because they are a good starting and end point for the experiment. The first genes for cold stress can be expected to be expressed from time point 15 minutes. After 4 days, the effects can also be measured over a long period of time.

To extract the relevant columns we use the function Frame.SliceCols

In [4]:

let relevantColumns = seq {"Cold_t_15_r_1_d_FALSE"; "Cold_t_15_r_2_d_FALSE"; "Cold_t_15_r_3_d_FALSE"; "Cold_t_5760_r_1_d_FALSE"; "Cold_t_5760_r_2_d_FALSE"; "Cold_t_5760_r_3_d_FALSE"}

let slicedData = Frame.sliceCols relevantColumns indexedFrame 
slicedData

		Cold_t_15_r_1_d_FALSE	Cold_t_15_r_2_d_FALSE	Cold_t_15_r_3_d_FALSE	Cold_t_5760_r_1_d_FALSE	Cold_t_5760_r_2_d_FALSE	Cold_t_5760_r_3_d_FALSE
		(int)	(int)	(int)	(int)	(int)	(int)
AT1G01010	->	21	13	12	41	43	36
AT1G01020	->	74	74	90	70	57	85
AT1G01030	->	23	23	42	26	22	29
AT1G01040	->	214	139	158	173	112	244
AT1G01050	->	242	268	215	332	262	313
:		...	...	...	...	...	...
ATMG09980	->	18	5	6	15	13	6
ATMG01370	->	4	19	22	64	40	30
ATMG01390	->	362	391	1019	1017	776	455
ATMG01400	->	0	1	0	1	0	0
ATMG01410	->	18	11	26	29	33	23

18873 rows x 6 columns

0 missing values

Do we have a Problem?¶

We will perform a transformation because we have a large data set and a log2 transformation allows to make the data more symmetric, reduces the variance and the linear relationship between the variables becomes easier to analyse.

Reminder: a log2 transformation, as we do here, makes it possible to reduce the bandwidth of a large group of data. That leads to a clearer analysis of our data.

You may think we can easily start here now, but you may have seen, that there are some zeros. Do we like the number zero? Not in our case, since we want to peform a log2 transformation!

But applying a log2 transformation of zero is not defined because the logarithm of zero is not defined and tends to -infinity

In our case, we cannot work with figures that approach -infinity.

So before the transformation we must add +1 to every value. So that every zero becomes +1, so that we avoid the problem of -infinity. That is because we want to calculate the Pearson correlation coefficient, which in turn calculates the arithmetic mean and standard deviation, the results also tend towards -infinity, which makes the results unusable

In [5]:

let slicedDataLog2 = 
    slicedData  
    |> Frame.mapValues (fun value -> log2 (value + 1.0))
slicedDataLog2

		Cold_t_15_r_1_d_FALSE	Cold_t_15_r_2_d_FALSE	Cold_t_15_r_3_d_FALSE	Cold_t_5760_r_1_d_FALSE	Cold_t_5760_r_2_d_FALSE	Cold_t_5760_r_3_d_FALSE
		(float)	(float)	(float)	(float)	(float)	(float)
AT1G01010	->	4.459431618637297	3.8073549220576037	3.700439718141092	5.392317422778761	5.459431618637297	5.20945336562895
AT1G01020	->	6.22881869049588	6.22881869049588	6.507794640198696	6.149747119504682	5.857980995127572	6.426264754702098
AT1G01030	->	4.584962500721157	4.584962500721157	5.426264754702098	4.754887502163469	4.523561956057013	4.906890595608519
AT1G01040	->	7.74819284958946	7.129283016944966	7.312882955284356	7.442943495848729	6.820178962415189	7.936637939002572
AT1G01050	->	7.924812503605781	8.071462362556625	7.754887502163469	8.379378367071263	8.038918989292302	8.294620748891626
:		...	...	...	...	...	...
ATMG09980	->	4.247927513443585	2.584962500721156	2.807354922057604	4	3.8073549220576037	2.807354922057604
ATMG01370	->	2.321928094887362	4.321928094887363	4.523561956057013	6.022367813028454	5.357552004618084	4.954196310386876
ATMG01390	->	8.50382573799575	8.614709844115207	9.994353436858859	9.991521846075695	9.60177078840771	8.832890014164743
ATMG01400	->	0	1	0	1	0	0
ATMG01410	->	4.247927513443585	3.5849625007211565	4.754887502163469	4.906890595608519	5.08746284125034	4.584962500721157

18873 rows x 6 columns

0 missing values

Pearson correlation coefficient¶

Definition¶

It calculates the correlation and thereby the strength and direction of the linear relationship between two variables in a dataset. It can assume values between -1 and 1. The formula for calculating the Pearson correlation coefficient is as follows.

$$ r = \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{(N-1) s_x s_y} = \frac{s_xy}{s_x s_y} $$

Let me explain the formula:

$x_i$ stands for the observed values for x.

In our case, the x-Values are the values in Column 0

$y_i$ stands for the individual observed values for our y-values.

In our data, the y-Values are the values in Columns 1

So x-values and y-values are the individual mearsured values of RNA concentration at a spefic point in time, which are compared with each other.

$\bar{x}$ and $\bar{y}$ stands for the arithmetic mean of x and y .

$\bar{x}$ and $\bar{y}$ therefore represent the average value of our data

$S_xy$ is the covariance.

The covariance primarily provides information about the direction of the correlation between x and y. It gives us an indication of how two variables change.

$S_x$ is the standard deviation of x.
$S_y$ is the standard deviation of y.

Example of Pearson correlation coeficient¶

Before we return to our data, i would like to explain how the Pearson correlation coefficient works using a simple example. Imagine we are examining two factors:

the hours devoted to studying and
the resulting scores on a test.

Our interest lies in uncovering any potential relationship between these variables.

Student	Hours studied	Test Score
Paul	2	60
Anna	3	70
Chris	5	75
Sophie	7	85
Mark	4	65

The result for our example is r = 0.93 is this a good result?

In [6]:

let xValues = [2.; 3.; 5.; 7.; 4.]
let yValues = [60.; 70.; 75.; 85.; 65.] 

let count = 5. // total numbers in both lists 
let sumX = List.sum xValues // addition of the numbers in xValues 
let sumY = List.sum yValues // addition of the numbers in yValues 

let sumXY =  
    List.map2 ( fun v1 v2 -> v1 * v2 ) xValues yValues // multiplication of variables of both lists 
    |> List.sum  // addition 

let sumXX = xValues |> List.map (fun x -> x ** 2.) |> List.sum // square every xValues
let sumYY = yValues |> List.map (fun y -> y ** 2.) |> List.sum // square every yValues

let cov = sumXY * count - sumX * sumY // calculating the covariance 

let deviationForX = sqrt ( count * sumXX  -  sumX **2.) // calculating the deviation for all the x
let deviationForY = sqrt ( count * sumYY  -  sumY **2.) // calculating the deviation for all the y 


let pearson = // calculating the Pearson correlation coefficient 
    cov / (deviationForX * deviationForY)
pearson

0.9324324324324325

In [7]:

let pearsonCorrelationExample = Correlation.Seq.pearson xValues yValues
pearsonCorrelationExample

0.9324324324324325

So as we see here our handwritten code and the function leads to the same result.

Interpretation of the example¶

What does the value 1 tell us now? It indicates that the correlation between two variables has a perfect linear relationship. In simpler terms, a value of +1 means that if we invest many hours in learning, we will also achieve a good grade

A value of -1 indicates that there is a perfect negative linear relationship between two variables. With a value of -1, less studying would lead to better grades.

A value of 0 defines that there is no linear relationship between variables. A value of 0 means that there is no relationship between the number of hours learned and the result. An example of this would be that a small young student's favourite colour is pink. Body size and favourite colour have

nothing to do with each other and
certainly nothing to do with the example of learning and the resulting grade.

So do we have a good example in the example above? This result indicates that there is a strong linear relationship between hours studied and the resulting grade.

Using the Pearson correlation coefficent¶

Using our example, the Pearson correlation coefficient is calculated for each column with all other columns.

For simplicity, let's look at the output of our next code. We get a matrix there we have 6 x 6 columns and take column zero and each value in column zero is compared to all values in column one and so on.

The matrix shows how similar the individual columns are to each other.

Digression - matrices¶

A matrix is a mathematical projection of a table that contains only numbers. They are used to describe linear transformation, among other things.
In our case we have a correlation matrix.
- represents the Pearson correlation coefficient between two variables. The matrix is symmetrical, i.e. a diagonal of perfect values is created.
- A column always correlates with itself, which in our case, and as we will see later, means that a value of +1 is always assumed there.

We take a step back, because what we have as headers of the columns are the individual replicas at different minutes.

This means we check how similar the replicates are to each other and how similar the measurement data is between the time intervals.

After understanding what the Person Coefficient is and how to calculate them lets go back to our data. In the next step we transfrom slicedDataLog2 into a matrix and calculate then the Pearson correlation coefficient. The output is a matrix of our six Columns from sliceDataLog2.

In [8]:

let transformSlicedDataLog2ToJaggedArray = 
    slicedDataLog2 
    |> Frame.toJaggedArray 
    |> matrix 

let pearsonCorrelationMatrix3 = 
    Correlation.Matrix.columnWiseCorrelationMatrix Correlation.Seq.pearson transformSlicedDataLog2ToJaggedArray
pearsonCorrelationMatrix3

		0	1	2	3	4	5
0	->	1.000	0.972	0.966	0.885	0.887	0.890
1	->	0.972	1.000	0.950	0.881	0.887	0.884
2	->	0.966	0.950	1.000	0.881	0.879	0.886
3	->	0.885	0.881	0.881	1.000	0.979	0.969
4	->	0.887	0.887	0.879	0.979	1.000	0.968
5	->	0.890	0.884	0.886	0.969	0.968	1.000

Matrix of 6 rows x 6 columns

Visualizing the Data¶

After applying Pearson correlation coefficient to all six of our columns, we can already draw our first conclusion.

First conclusion¶

We see here a lot of numbers between 0 and +1. So we can say that there is a positive linearity between the individual columns.

Since graphics are much nicer and can also better represent the similarity, we create a so-called Heatmap that represents the Pearson correlation coefficient or the correlation between our individual columns.

In [9]:

let matrixToJaggedArray = 
    pearsonCorrelationMatrix3
    |> Matrix.toJaggedArray
let HeatMap = 
    Chart.Heatmap (zData = matrixToJaggedArray, colNames = ["15_minutes_R_1"; "15_minutes_R_2"; "15_minutes_R_3"; "4_days_R_1"; "4_days_R_2"; "4_days_R_3"], rowNames = ["15_minutes_R_1"; "15_minutes_R_2"; "15_minutes_R_3"; "4_days_R_1"; "4_days_R_2"; "4_days_R_3"] )

let StylingHeatMap = 
    HeatMap
    |> Chart.withTitle ("Heatmap - Coldstress Experiment - 15 Minutes & 4 Days")
    |> Chart.withSize(1000,900)
    |> Chart.withMarginSize(Bottom = 200, Right = 200, Left = 200)
StylingHeatMap

Interpreting the visualisation¶

Looks cool huh? But now let's move on to the interpretation.

If we take a closer look, we will notice a lot of boxes that correspond either to the yellow-orange tones or the blue tones. What we see here is quiete simple. On X- and Y-Axis we have our six Columns:

Three replicates for minute 15
Three replicates for 4 days

and now we see here coded in colors what the Pearson correlation coefficient does.

Lets start in the left bottom corner with 15_minutes_R_1. When we look at the legend we see that this field corresponds to the value 1 wich is the best value we can get. This is because here were the values of 15_minutes_R_1 compared with itself, as the values are identical this results in a maximum Pearson correlation coefficient.

If we move to 15_minutes_R_2, we see from the colour here, this box is assigned a value of 0.97. This result is also a high Pearson correlation coefficient, so that means the results are very similar to each other. But what was compared here? Quite simply 15_minutes_R_1 with 15_minutes_R_2.

Now let's take a look at 4_days_R_1. What is immediately noticeable here is that it is blue and therefore corresponds to a value of 0.88.

In our case, this tells us that 4_days_R_1 is less similar to 15_minutes_R_1

This box is the result of the comparison between 15_minutes_R_1 and 4_days_R_1, but why is there such a difference here? Because we are working with replicates - 15_minutes_R_1 was measured at 15 minutes and 4_days_R_1 at 5760 minutes.

Conclusion¶

We generally assume that A. thaliana changes its behaviour when the plant comes into contact with the cold. For this we used a method called RNA-Seq. We compared two replicate groups at different time points and expected our replicate groups to differ. To do this, we calculated the Pearson correlation coefficient and created a heat map.

Results¶

The Pearson correlation matrix and the associated heat map show that there are some differences between the replicate groups. However, these differences are small. The differences within the individual replicate groups are also small. These small differences between and within the replicate groups indicate a linear relationship both between the replicate groups and between the individual replicates within the groups. This leads to the conclusion that the replicate groups and the individual replicates within these groups have a high consistency and similarity. This suggests that the data are robust and reliable, which is important for further analyses and interpretations.

Pearson correlation coefficient, Correlation Matrices and Heatmap

Posted on 2024-5-17 by Pauline Hans in Data Science

Pearson correlation coefficient, Correlation Matrices and Heatmap¶

Introduction:¶

What is a RNA-Seq?¶

The Experiment¶

What we expect¶

Lets get ready to rumble:¶

Start of the Journey¶

Dataframe 2.0¶

Do we have a Problem?¶

Pearson correlation coefficient¶

Definition¶

Example of Pearson correlation coeficient¶

Interpretation of the example¶

Using the Pearson correlation coefficent¶

Digression - matrices¶

Visualizing the Data¶

First conclusion¶

Interpreting the visualisation¶

Conclusion¶

Results¶